In mathematics, a natural number in a given number base is a -Kaprekar number if the representation of its square in that base can be split into two parts, where the second part has digits, that add up to the original number. For example, in base 10, 45 is a 2-Kaprekar number, because 45² = 2025, and 20 25 = 45. The numbers are named after D. R. Kaprekar.
Definition and properties
Let be a natural number. Then the Kaprekar function for base and power is defined to be the following:
- ,
where and
A natural number is a -Kaprekar number if it is a fixed point for , which occurs if . and are trivial Kaprekar numbers for all and , all other Kaprekar numbers are nontrivial Kaprekar numbers.
The earlier example of 45 satisfies this definition with and , because
A natural number is a sociable Kaprekar number if it is a periodic point for , where for a positive integer (where is the th iterate of ), and forms a cycle of period . A Kaprekar number is a sociable Kaprekar number with , and a amicable Kaprekar number is a sociable Kaprekar number with .
The number of iterations needed for to reach a fixed point is the Kaprekar function's persistence of , and undefined if it never reaches a fixed point.
There are only a finite number of -Kaprekar numbers and cycles for a given base , because if , where then
and , , and . Only when do Kaprekar numbers and cycles exist.
If is any divisor of , then is also a -Kaprekar number for base .
In base , all even perfect numbers are Kaprekar numbers. More generally, any numbers of the form or for natural number are Kaprekar numbers in base 2.
Set-theoretic definition and unitary divisors
The set for a given integer can be defined as the set of integers for which there exist natural numbers and satisfying the Diophantine equation
- , where
An -Kaprekar number for base is then one which lies in the set .
It was shown in 2000 that there is a bijection between the unitary divisors of and the set defined above. Let denote the multiplicative inverse of modulo , namely the least positive integer such that , and for each unitary divisor of let and . Then the function is a bijection from the set of unitary divisors of onto the set . In particular, a number is in the set if and only if for some unitary divisor of .
The numbers in occur in complementary pairs, and . If is a unitary divisor of then so is , and if then .
Kaprekar numbers for
b = 4k 3 and p = 2n 1
Let and be natural numbers, the number base , and . Then:
- is a Kaprekar number.
- is a Kaprekar number for all natural numbers .
b = m2k m 1 and p = mn 1
Let , , and be natural numbers, the number base , and the power . Then:
- is a Kaprekar number.
- is a Kaprekar number.
b = m2k m 1 and p = mn m − 1
Let , , and be natural numbers, the number base , and the power . Then:
- is a Kaprekar number.
- is a Kaprekar number.
b = m2k m2 − m 1 and p = mn 1
Let , , and be natural numbers, the number base , and the power . Then:
- is a Kaprekar number.
- is a Kaprekar number.
b = m2k m2 − m 1 and p = mn m − 1
Let , , and be natural numbers, the number base , and the power . Then:
- is a Kaprekar number.
- is a Kaprekar number.
Kaprekar numbers and cycles of for specific ,
All numbers are in base .
Extension to negative integers
Kaprekar numbers can be extended to the negative integers by use of a signed-digit representation to represent each integer.
See also
- Arithmetic dynamics
- Automorphic number
- Dudeney number
- Factorion
- Happy number
- Kaprekar's constant
- Meertens number
- Narcissistic number
- Perfect digit-to-digit invariant
- Perfect digital invariant
- Sum-product number
Notes
References
- D. R. Kaprekar (1980–1981). "On Kaprekar numbers". Journal of Recreational Mathematics. 13: 81–82.
- M. Charosh (1981–1982). "Some Applications of Casting Out 999...'s". Journal of Recreational Mathematics. 14: 111–118.
- Iannucci, Douglas E. (2000). "The Kaprekar Numbers". Journal of Integer Sequences. 3: 00.1.2. Bibcode:2000JIntS...3...12I.
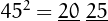

![D R Kaprekar (Indian Mathematician) Bio with [ Photos Videos ]](http://www.hobbyshobby.com/Crossword/Images/DR_Kaprekar_xw.png)


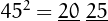

![D R Kaprekar (Indian Mathematician) Bio with [ Photos Videos ]](http://www.hobbyshobby.com/Crossword/Images/DR_Kaprekar_xw.png)
